
设计师软考中级笔记——2.程序设计语言基础
本章将学习:
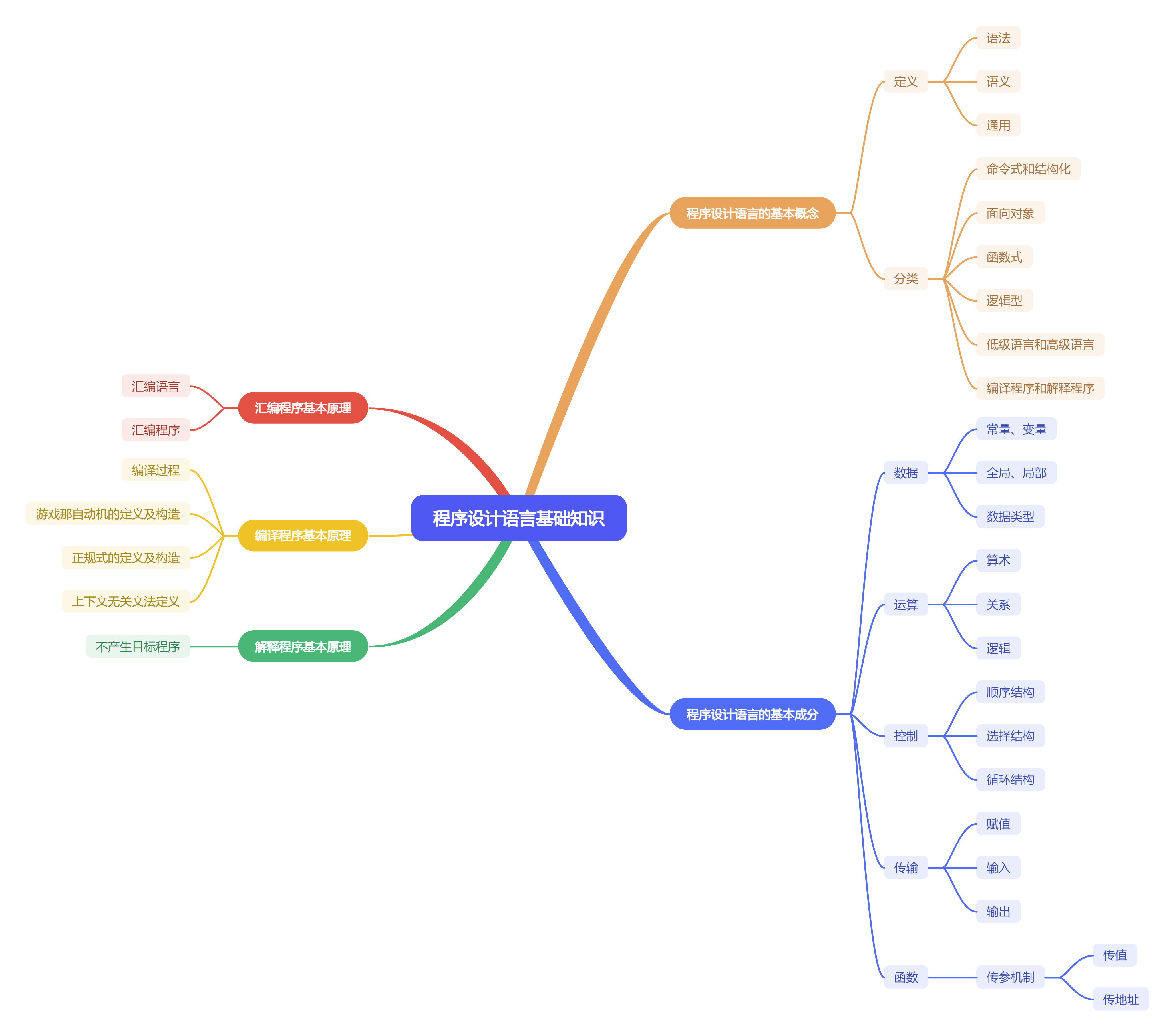
编程语言的基本概念
低级与高级语言
- 低级语言:汇编
- 高级语言:常见的有
Java、C、C++、PHP、Python、Delphi等- 翻译形式:汇编、解释、编译
- 程序设计语言的定义:语法、语义、语用
- 程序设计语言的分类
- 过程式(命令式和结构化):FORTRAN、Pacscal、C
- 面向对象:Java、Python、C++
- 函数式:lisp、python、scala
- 逻辑型:prolog
- 脚本语言:shell、bat、js、python
程序设计的基本成分
程序设计的基成分包括:数据、运算、控制和传输等。
- 数据成分
- 常量和变量
- 全局量和局部量
- 数据类型
- 运算成分:算式运算、关系运算、逻辑运算
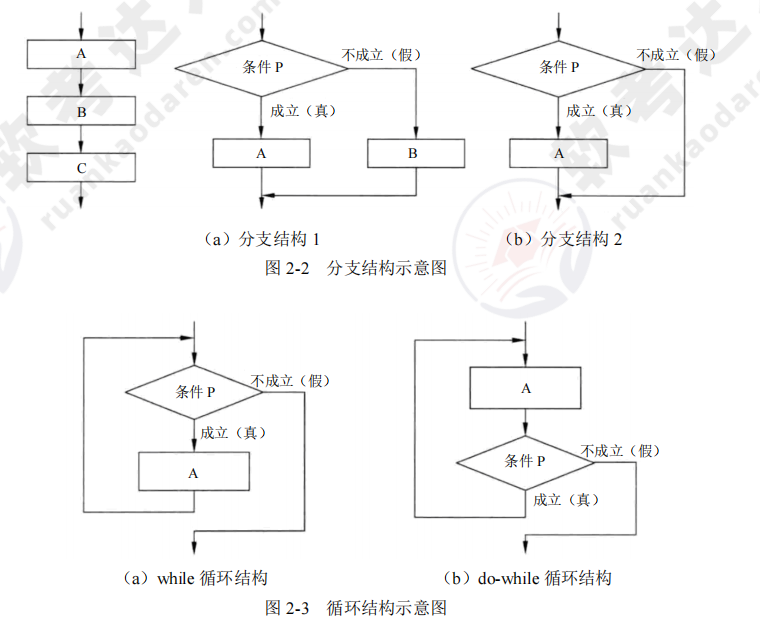
- 控制成分:顺序结构、选择结构、循环结构
控制成分的结构图如下:
汇编程序基本原理
汇编语言
汇编语言是为特定的计算机或计算机系统设计的面向机器符号化的程序设计语言。
用汇编语言编写的程序称为汇编语言源程序。因为计算机不能直接识别和运行符号语言程序,所以要用专门的翻译程序——汇编程序进行翻译。
汇编程序也编写程序要遵循所用语言的规范和约定。
汇编语言源程序由若干条语句组成,一个程序中可以有三类语句:指令语句、伪指令语句和宏指令语句。
汇编程序
将汇编语言所编写的源程序翻译成机器指令程序。汇编程序一般需要两次扫描源程序才能完成翻译过程。
- 第一次扫描:检查语法错误,确定符号名字;建立使用的全部符号名字表;每一符号名字后跟一对应值(地址或数)。
- 第二次扫描:在第一次扫描的基础上,将符号地址转换成真地址(代真);利用操作码表将助记符转换成相应的目标码。
编译程序基本原理
编译程序
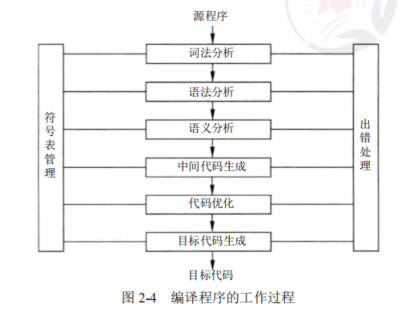
编译程序的工作过程分为六个阶段,如下:
文法
定义:文法是一种形式化工具,用一组规则定义语言的语法结构,规定了如何由单词和符号构成合法的句子、表达式或程序等,让计算机和人能理解、生成符合规则的语句。
一个形式文法是一个有序四元组,如下:
G={Vn,Vt,S,P}- Vn:非终结符号;部署语言组成部分,不是最终结果,可理解为占位符
- Vt:终结符;是语言的组成部分,是最终结果。
- S:起始符;是语言的开始符号。
- P:产生式;用终结符替代非终结符的规则。
同时,有时候为了方便也不会添加下标,就会是“G={V, T, S, P}”
| 类型 | 别称 | 对应自动机 |
|---|---|---|
| 0型 | 短语文法 | 图灵机 |
| 1型 | 上下文有关文法 | 线性界限自动机 |
| 2型 | 上下文无关文法 | 非确定的下推自动机 |
| 3型 | 正规文法 | 有限自动机 |
语法推导树
一颗语法树应该具有以下特征:
- 每个结点都有一个标记,此标记是V的一个符号
- 根的标记是S
- 若一结点n至少有一个它自己除外的子孙,并且有标记A,则A肯定在Vn中
- 如果结点n的直接子孙,从左到右次序是结点n1,n2,...nk,其标记分别是:A1, A2, A3...A
举例:
文法G=({a,b},{S,A},S,P)其中:
S->aAs|a
A->SbA|SS|ba
请构造句型aabAa
推导过程:
- 总结方法:尽可能的将构造句型以树的形式完成
- aabAa
- 这个a首先选择的是 aAs|a,因为句型中需要A
aabAa- 进入第一次递归,这个A选择的是 SbA|SS|ba,因为需要一个b和A,如果使用ba的话,A就没了
- aabAa
- 最终的树图如下:
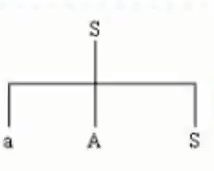


有限自动机
自动机是一种抽象的计算模型,它能够按照一定的规则对输入的符号串进行处理,并根据处理结果进入不同的状态。
为什么需要自动机
- 应对复杂状态变迁`
在编程中,像用户交互、网络传输、硬件控制等场景,往往存在着大量的状态转换情况。
拿TCP举例,它有建立连接、数据传输、连接关闭等多种状态,而且不通过状态之间的转换规则非常繁琐。
如果使用自动机,自动机将通过定义清晰的状态、输入以及转移规则,能够把这些复杂的逻辑变得有条理。 - 提升代码可维护性
将状态逻辑从业务代码中分离出来,能够让代码的结构更加清晰,便于后续的修改和扩展。例如,在游戏开发中,角色的状态(如 Idle、Run、Jump)可以通过自动机来管理,每个状态对应的行为都能独立实现。
有限自动机
计算机控制系统的控制程序具有有限状态自动机(FA)的特征,可以用有限状态机理论来描述。
-
确定的有限自动机(DFA):该状态机在任何一个状态,基于输入的字符都能做成一个确定的状态转换
- 一个确定的有限自动机是个五元组(S,∑,f,s0,Z),其中:
- S:一个有限集,其每个元素称为一个状态。
- ∑:一个有穷字母表,其每个元素称为一个输入字符。
- f:是S*∑->S上的单值部分映像
- s0∈S,是唯一的一个开始状态。
- Z 是非空的终止状态集合,Z⊆S。
- 一个确定的有限自动机是个五元组(S,∑,f,s0,Z),其中:
-
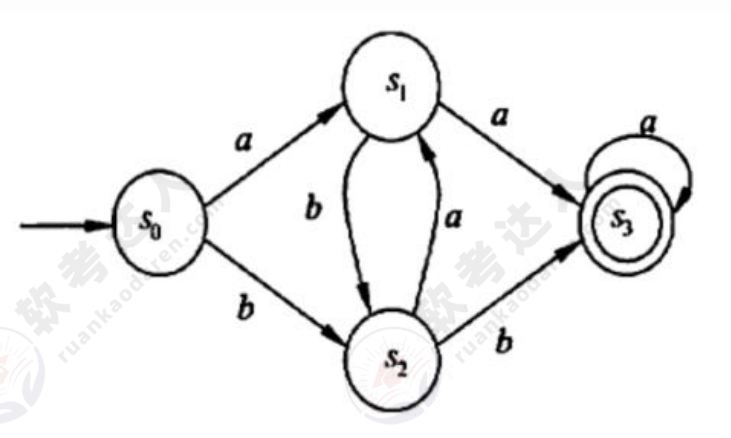
不确定的有限自动机(NFA):该状态机在任何一个状态,基于输入的字符都不能做成一个确定的状态转换。
- 对于一个输入,它可以有两个状态可以转换
- 存在ε的情况,即没有任何字符输入的情况下,NFA可以从一个状态迁移到另一个状态。
- 感谢你赐予我前进的力量
赞赏者名单
因为你们的支持让我意识到写文章的价值🙏
本文是原创文章,采用 CC BY-NC-ND 4.0 协议,完整转载请注明来自 zxb
评论
隐私政策
你无需删除空行,直接评论以获取最佳展示效果






-ienecves.png)
-yqcolaqh.png)

