什么是冒泡排序

冒泡排序的英文Bubble Sort，是一种基础的交换排序。
这种排序算法的每一个元素都可以像小气泡一样，根据自身大小，一点一点向着数组的一侧移动。

举个例子，将一个无需数列5, 8, 6, 3, 9, 2, 1, 7，从小到大排序

排序流程图

最外层的 for 循环每经过一轮，剩余数字中的最大值就会被移动到当前轮次的最后一位，中途也会有一些相邻的数字经过交换变得有序。

第一轮排序：



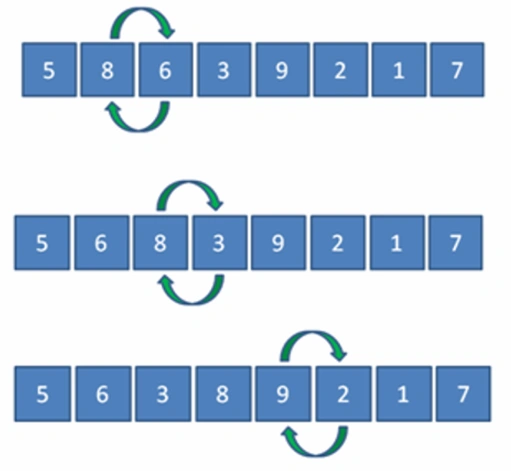
第二轮排序


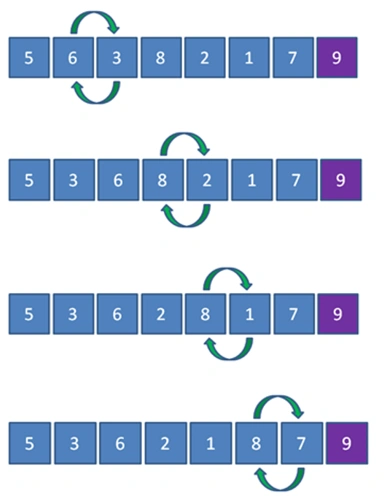
三到七轮结果

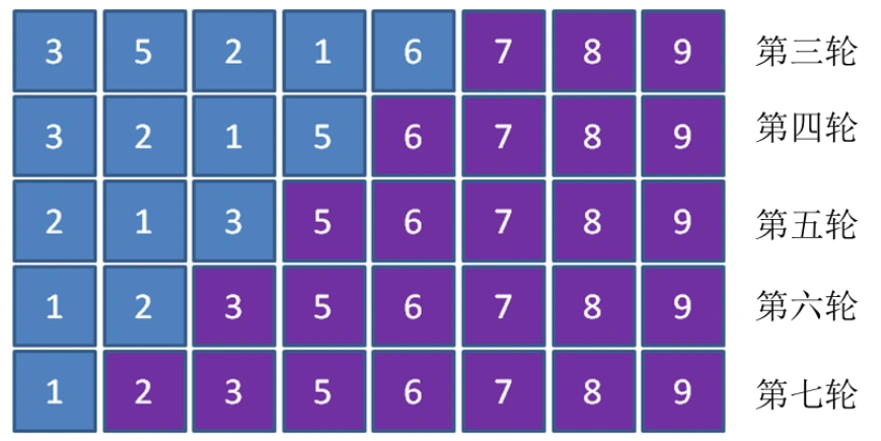
算法实现

基础实现

冒泡最基础的实现方式如下：

public class BubbleSort {
    public static int[] sort1(int array[]) {
        for (int i = 0; i < array.length; i++) {
            for (int j = 0; j < array.length - 1 - i; j++) { // arr.length - 1 - i：数组遍历i之后的大小 
                if (array[j] > array[j + 1]) { // 如果左边的数大于右边，则交换
                    int tmp = array[j];
                    array[j] = array[j + 1];
                    array[j + 1] = tmp;
                }
            }
        }
        return array;
    }
}

改良实现

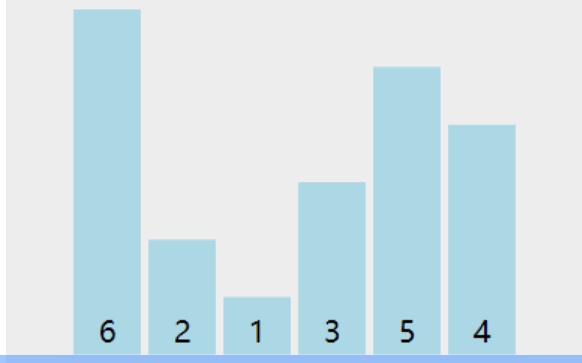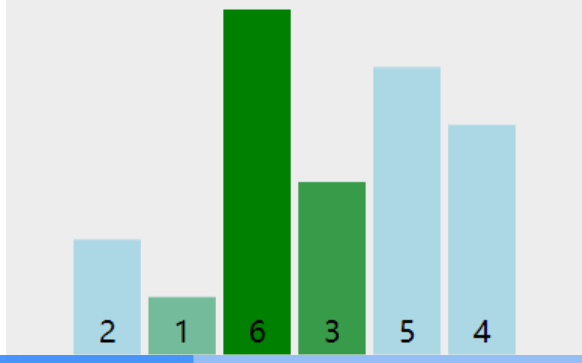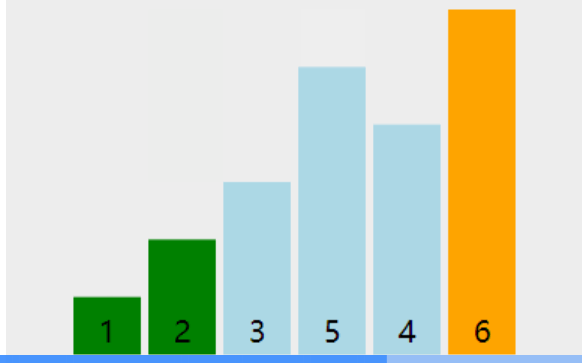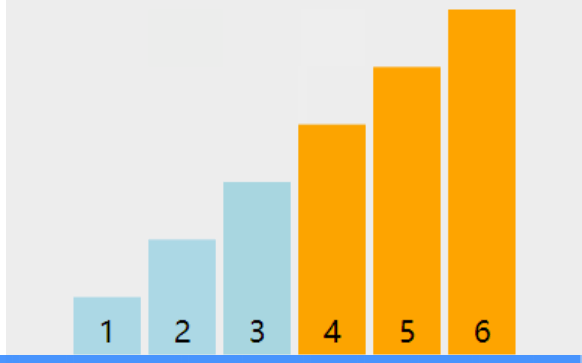
如上图，在每次的外层循环时，进行判断，如果没有发生过交换，那么此时数组就是有序，则可以不用继续循环。

public void sort2() {  
    int[] arr = {3, 5, 4, 2, 1};  
    boolean swapped;  
    for (int i = 0; i < arr.length; i++) {  
        swapped = false;  
        for (int j = 0; j < arr.length - 1 - i; j++) {  
            if (arr[j] > arr[j + 1]) {  
                int tmp = arr[j];  
                arr[j] = arr[j + 1];  
                arr[j + 1] = tmp;  
                swapped = true;  
            }  
        }  
        if (!swapped) break;  
    }  
    System.out.println(Arrays.toString(arr));  
}

进一步优化代码：

public void sort3() {  
    int[] arr = {3, 5, 4, 2, 1};  
    boolean swapped = true;  
    int indexOfLastUnosortedElement = arr.length - 1;  
    int swappedIndex = -1;  
    while(swapped) {  
        swapped = false;  
        for (int i = 0; i < indexOfLastUnosortedElement; i++) {  
           if (arr[i] > arr[i + 1]) {  
               int tmp = arr[i];  
               arr[i] = arr[i + 1];  
               arr[i + 1] = tmp;  
               swapped = true;  
               swappedIndex = i; // 更新交换位置
           }  
        }  
        indexOfLastUnosortedElement = swappedIndex;  
    }  
    System.out.println(Arrays.toString(arr));  
}

最外层的 while 循环每经过一轮，剩余数字中的最大值仍然是被移动到当前轮次的最后一位。

在下一轮比较时，只需比较到上一轮比较中，最后一次发生交换的位置即可。因为后面的所有元素都没有发生过交换，必然已经有序了。