排序算法——选择排序

选择排序：双重循环遍历数组，每经过一轮比较，找到最小元素的下标,，将其交换至首位。

int[] arr = {3, 5, 4, 2, 1};  
@Test  
public void selectionSort() {  
    int minIndex;  
    for (int i = 0; i < arr.length - 1; i++) {  
        minIndex = i;  
        for (int j = i + 1; j < arr.length; j++) {  
            if (arr[minIndex] > arr[j]) minIndex = j;  
        }  
        int temp = arr[i];  
        arr[i] = arr[minIndex];  
        arr[minIndex] = temp;  
    }  
    System.out.println(Arrays.toString(arr));  
}

动图演示：

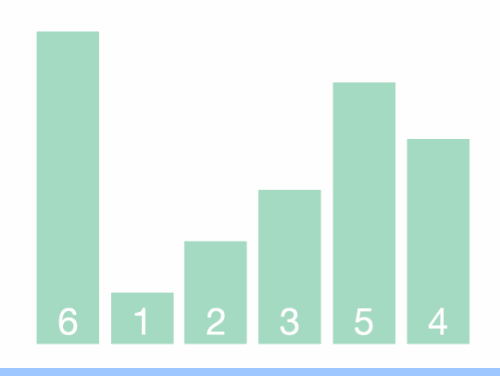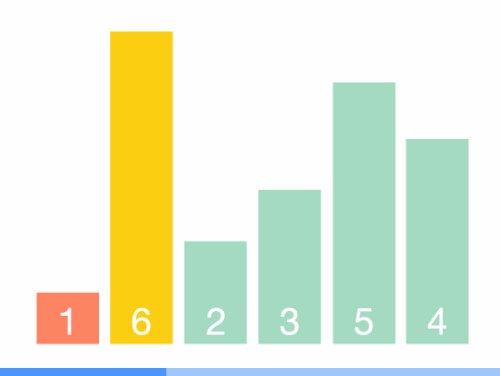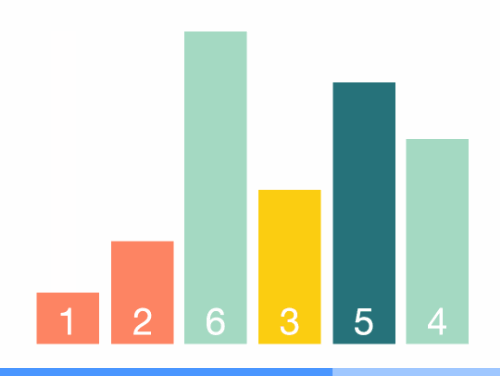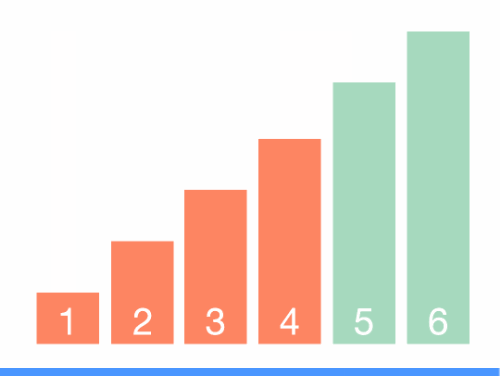
那么，选择排序和冒泡排序有什么异同？

相同点：

• 都是两层循环，时间复杂度都为 $O(n^2)$
• 都只使用有限个变量，空间复杂度为 $O(1)$

不同点：

• 冒泡排序在比较过程中就不断变换
• 选择排序，只有在遍历完最内层才会进行交换
• 冒泡排序是稳定的，而选择排序是不稳定的

排序算法的稳定性

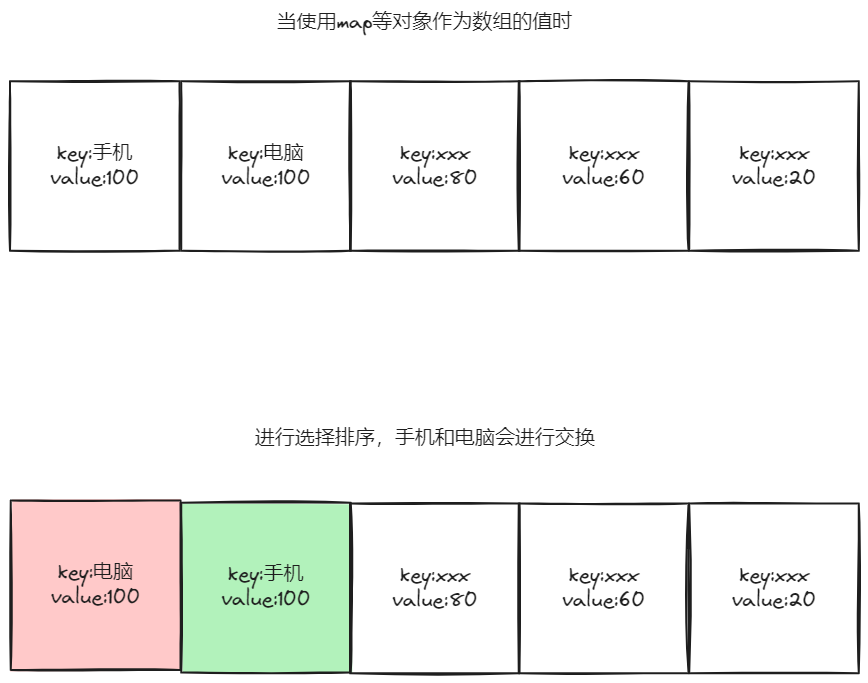
工具上图可知，如果使用选择排序时，由于minIdex最终会将相同值但不同key的对象进行调换，因此该排序的稳定性弱于冒泡排序，也称为不稳定的排序。

当然，这也不是绝对的，当将冒泡排序的条件“左边的数大于右边的数时，则交换”改为“左边的数大于或等于右边的数，则交换” ，算法就变成不稳定的了。

优化方式：“新开一个数组，将每轮找出的最小值依次添加到新数组中，选择排序算法就变成稳定的了。”

二元选择排序

选择排序算法也是可以优化的，二元选择排序将 最大值和最小值同时都找出。

@Test  
public void selectionSort2() {  
    int minIndex, maxIndex;  
    // i 只需要遍历一半  
    for (int i = 0; i < arr.length / 2; i++) {  
        minIndex = i;  
        maxIndex = i;  
        for (int j = i + 1; j < arr.length - i; j++) {  
            if (arr[minIndex] > arr[j]) {  
                // 记录最小值的下标  
                minIndex = j;  
            }  
            if (arr[maxIndex] < arr[j]) {  
                // 记录最大值的下标  
                maxIndex = j;  
            }  
        }  
        // 如果 minIndex 和 maxIndex 都相等，那么他们必定都等于 i，且后面的所有数字都与 arr[i] 相等，此时已经排序完成  
        if (minIndex == maxIndex) break;  
        // 将最小元素交换至首位  
        int temp = arr[i];  
        arr[i] = arr[minIndex];  
        arr[minIndex] = temp;  
        // 如果最大值的下标刚好是 i，由于 arr[i] 和 arr[minIndex] 已经交换了，所以这里要更新 maxIndex 的值。  
        if (maxIndex == i) maxIndex = minIndex;  
        // 将最大元素交换至末尾  
        int lastIndex = arr.length - 1 - i;  
        temp = arr[lastIndex];  
        arr[lastIndex] = arr[maxIndex];  
        arr[maxIndex] = temp;  
    }  
    System.out.println(Arrays.toString(arr));  
}